Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. M adalah titik
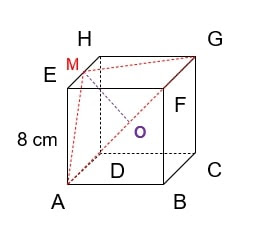
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. M adalah titik tengah EH. Jarak titik M ke AG adalah ....
- $4\sqrt{6}cm$.
- $4\sqrt{5}cm$.
- $4\sqrt{3}cm$.
- $4\sqrt{2}cm$.
- $4cm$.
PEMBAHASAN:
Agar mudah dalam menghitung, cobalah gambar kubus ABCD.EFGH terlebih dulu dan tambahkan garis bantu yang menghubungkan titik-titik yang diketahui pada soal.
Jika sudah digambar, sekarang kita lihat, dan pilih pola segitiga yang dapat kita hitung dengan teorema pytagoras.
Misal, disini saya mengambil segitiga AEM yang sudah diketahui dua nilai sisinya, tinggal mencari nilai hipotenusa (AM).
$\begin{align*} MA^{2} &= 4^{2}+8^{2} \\ MA^{2} &= 16+64\\ MA &= \sqrt{80}=4\sqrt{5} \end{align*}$Setelah mengetahui nilai MA, cari nilai AO. Karena AO bernilai 1/2 diagonal ruang, nilai AO dapat diketahui yaitu $4\sqrt{3}cm$
Setelah dua nilai ditemukan, kita bisa menghitung jarak titik M ke O (titik AG) menggunakan phytagoras.
$\begin{align*} MO^{2} &= (4\sqrt{5})^{2}-(4\sqrt{3})^{2}\\ MO^{2} &= 80-48\\ MO &= \sqrt{32} = 4\sqrt{2}\\ \end{align*}$Jadi, jarak titik M ke AG adalah $4\sqrt{2}cm$.
JAWABAN: D